Second of Five Lagrangian Equilibrium Points

The more I thought about it, the more it made sense that one image we're getting, is quite different(lensing) from the image that is behind the brane? The idea of brane collision from steinhardt and turok perspective, created this space bewteen the branes, while the image behind this(the other image) is receding?

I am not sure exactly.

Dark matter in the high-redshift cluster CL 0152-1357. Gravitational lensing analysis with the Advanced Camera for Surveys (ACS) reveals the complicated dark matter distribution (purple) in unprecedented detail when the Universe was at half its present age. The yellowish galaxies are the visible cluster member galaxies forming a filamentary structure, possibly in the process of merging.
(Jee et al. 2005, Astrophysical Journal)

Not many can see in this abstract way, or have considered how a photon might have travelled? Sure they have understood satellites and the travel through space, but have they consider this in context of CSL lensing? Sean put up a link yesterday that had me seeing how such a travel over distance might have had some photonic strange journies in context of such lensings.



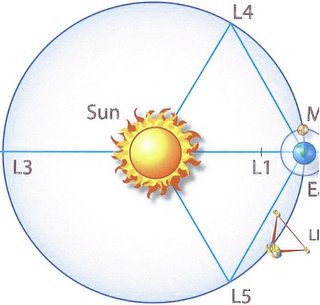
The second of five Lagrangian equilbrium points, approximately 1.5 million kilometers beyond Earth, where the gravitational forces of Earth and Sun balance to keep a satellite at a nearly fixed position relative to Earth.

This picture below really set the final stage for me. Thus simplification has been mounted in how we see such tubes formed within the greater context of the universe and here we have a way of seeing that is new? It helps one to view universe travel and paves the way for roads through such space?

Is it so hard to visualize? Is it so hard not to consider how one should make there way through such space?


Weak Lensing Distorts Universe?

IN order to extend the link to the information supplied in previous article presented by Sean Carroll, Fraser Cain here links us to the following conversation.

Feynman's Path Integrals

While this following comment might seem inappropriate to the content of this post, I place it because of what I see in determination of the langangian methods used to help us see how gravitatonal equilibrium points, speak to how such travels would have been initiated in sum over paths used as Feynman's distributes the actions according to set model held i a cosmological sense I am looking at the the picture above here and the path ways shown.

December 15th, 2005 at 2:35 pm
Tony Smith:


As to the time of Feynman soving the QED problem, in 1941 (according to Mehra’s Feynman biography The Beat of a Different Drum (Oxford 1994)) Feynman had the inspiration from Dirac’s paper of using the Lagrangian method, which led to Feynman’s 1942 Ph.D. thesis. As to that thesis, Mehra says “… Feynman mentioned that “the problem of the form that relativistic quantum mechanics, and the Dirac equation, take from this point of view, remains unsolved. …”. So, Feynman’s Shelter Island relativistic QED solution was developed after his 1942 Ph.D. thesis.

I had been looking for this relationship and how Feynman’s toys models came into being? Can this be the beginning as you relate?