Theoretical Excellence

Although Aristotle in general had a more empirical and experimental attitude than Plato, modern science did not come into its own until Plato's Pythagorean confidence in the mathematical nature of the world returned with Kepler, Galileo, and Newton. For instance, Aristotle, relying on a theory of opposites that is now only of historical interest, rejected Plato's attempt to match the Platonic Solids with the elements -- while Plato's expectations are realized in mineralogy and crystallography, where the Platonic Solids occur naturally.Plato and Aristotle, Up and Down-Kelley L. Ross, Ph.D.

This is the first introduction then that is very important to me about what is perceived as a mathematical framework. So it is not such an effort to think about our world and think hmmmm.... a mathematical abstract of our reality is there to be discovered. I first noticed this attribute in Pascal's triangle.

Nineteenth Century Geometry by Roberto Torretti

The sudden shrinking of Euclidean geometry to a subspecies of the vast family of mathematical theories of space shattered some illusions and prompted important changes in our the philosophical conception of human knowledge. Thus, for instance, after these nineteenth-century developments, philosophers who dream of a completely certain knowledge of right and wrong secured by logical inference from self-evident principles can no longer propose Euclidean geometry as an instance in which a similar goal has proved attainable. The present article reviews the aspects of nineteenth century geometry that are of major interest for philosophy and hints in passing, at their philosophical significance.

While I looked further into the world of Pythagorean developments I wondered how such an abstract could have ever lead to the world of non-euclidean geometries. There is this progression of the geometries that needed to be understood. It included so many people that we only now acknowledge the greatest names but it is in the exploration of "theoretical excellence" that we gain access to the spirituality's of the mathematical world.

"I’m a Platonist — a follower of Plato — who believes that one didn’t invent these sorts of things, that one discovers them. In a sense, all these mathematical facts are right there waiting to be discovered."Donald (H. S. M.) Coxeter

While some would wonder what value this exploration into such mathematical abstracts, how could we describe for ourselves the ways things would appear at such levels microscopically reduced, has an elemental quality to it? Yes, I have gone to one extreme, and understand, it included so many different mathematics, how could we ever understand this effort and assign it's rightful place in history? Theoretics then, is this effort?

How Strange the elements of our world?

The crystalline state is the simplest known example of a quantum , a stable state of matter whose generic low-energy properties are determined by a higher organizing principle and nothing else. Robert Laughlin

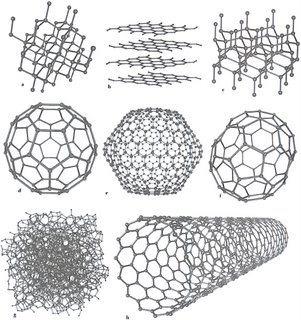
This illustration depicts eight of the allotropes (different molecular configurations) that pure carbon can take:

a) Diamond
b) Graphite
c) Lonsdaleite
d) Buckminsterfullerene (C60)
e) C540
f) C70
g) Amorphous carbon
h) single-walled carbon nanotube

Review of experiments

Graphite exhibits elastic behaviour and even improves its mechanical strength up to the temperature of about 2500 K. Measured changes in ultrasonic velocity in graphite after high temperature creep shows marked plasticity at temperatures above 2200 K [16]. From the standpoint of thermodynamics, melting is a phase transition of the first kind, with an abrupt enthalpy change constituting the heat of melting. Therefore, any experimental proof of melting is associated with direct recording of the temperature dependence of enthalpy in the neighbourhood of a melting point. Pulsed heating of carbon materials was studied experimentally by transient electrical resistance and arc discharge techniques, in millisecond and microsecond time regime (see, e.g., [17, 18]), and by pulsed laser heating, in microsecond, nanosecond and picosecond time regime (see, e.g., [11, 19, 20]). Both kind of experiments recorded significant changes in the material properties (density, electrical and thermal conductivity, reflectivity, etc. ) within the range 4000-5000 K, interpreted as a phase change to a liquid state. The results of graphite irradiation by lasers suggest [11] that there is at least a small range of temperatures for which liquid carbon can exist at pressure as low as 0.01 GPa. The phase boundaries between graphite and liquid were investigated experimentally and defined fairly well.

Solidification of Geometrical Presence

While I might infer the "attributes of Coxeter here," it is with the understanding such a dimensional perspective which has it's counterpart in the result of what manifests as matter creations. Yet we have taken our views down to the "powers of ten" to think of what could manifest even before we see the result in nature.

When you go to the site by PBS of where, Nano: Art Meets Science, make sure you click on the lesson plan to the right.



Buckyballs

Visitors' shadows manipulate and reshape projected images of "Buckyballs." "Buckyball," or a buckminsterfullerene molecule, is a closed cage-structure molecule with a carbon network. "Buckyball" was named for R. Buckminster "Bucky" Fuller (1895-1983), a scientist, philosopher and inventor, best known for creating the geodesic dome.
Photo Credit: © 2003 Museum Associates/Los Angeles County Museum

Fundamentally the properties of materials can be changed by nanotechnology. We can arrange molecules in a way that they do not normally occur in nature. The material strength, electronic and optical properties of materials can all be altered using nanotechnology.

See Related information on bucky balls here in this site. This should give some understanding of how I see the greater depth of what manifest in nature, as solids in our world, has some "other" possibilities in dimensional attribute, while it is given association to the mathematical prowess of E8.

I do not know of many who will take in all that I have accumulated in regards to how one may look at their planet, can have the depth of perception that is held in to E8.?

One may say what becomes of the world as it manifest into it's constituent parts, has this energy relation, that it would become all that is in the design of the world around us.



While some scientists puzzle as to the nature of the process of E8, little did they realize that if you move your perception to the way E8 is mapped to 248 dimensions, the image while indeed quite pleasing, you see as a result.

It can include so much information, how would you know that this object of mathematics, is a polytrope of a kind that is given to the picture of science in the geometrical structure of the bucky ball or fullerene.

Allotropes



Diamond and graphite are two allotropes of carbon: pure forms of the same element that differ in structure.

Allotropy (Gr. allos, other, and tropos, manner) is a behaviour exhibited by certain chemical elements: these elements can exist in two or more different forms, known as allotropes of that element. In each different allotrope, the element's atoms are bonded together in a different manner.

For example, the element carbon has two common allotropes: diamond, where the carbon atoms are bonded together in a tetrahedral lattice arrangement, and graphite, where the carbon atoms are bonded together in sheets of a hexagonal lattice.

Note that allotropy refers only to different forms of an element within the same phase or state of matter (i.e. different solid, liquid or gas forms) - the changes of state between solid, liquid and gas in themselves are not considered allotropy. For some elements, allotropes can persist in different phases - for example, the two allotropes of oxygen (dioxygen and ozone), can both exist in the solid, liquid and gaseous states. Conversely, some elements do not maintain distinct allotropes in different phases: for example phosphorus has numerous solid allotropes, which all revert to the same P4 form when melted to the liquid state.

The term "allotrope" was coined by the famous chemist Jöns Jakob Berzelius.

Pasquale Del Pezzo and E8 Origination?

"I’m a Platonist — a follower of Plato — who believes that one didn’t invent these sorts of things, that one discovers them. In a sense, all these mathematical facts are right there waiting to be discovered."Donald (H. S. M.) Coxeter

There are two reasons that having mapped E8 is so important. The practical one is that E8 has major applications: mathematical analysis of the most recent versions of string theory and supergravity theories all keep revealing structure based on E8. E8 seems to be part of the structure of our universe.

The other reason is just that the complete mapping of E8 is the largest mathematical structure ever mapped out in full detail by human beings. It takes 60 gigabytes to store the map of E8. If you were to write it out on paper in 6-point print (that's really small print), you'd need a piece of paper bigger than the island of Manhattan. This thing is huge.

Clifford of Asymptotia drew our attention to this for examination and gives further information and links with which to follow.

He goes on to write,"Let’s not get carried away though. Having more data does not mean that you worked harder to get it. Mapping the human genome project involves a much harder task, but the analogy is still a good one, if not taken too far."

Of course since the particular comment of mine was deleted there, and of course I am okay with that. It did not mean I could not carry on here. It did not mean that I was not speaking directly to the way these values in dimensional perspective were not being considered.

Projective Geometries?

A theorem which is valid for a geometry in this sequence is automatically valid for the ones that follow. The theorems of projective geometry are automatically valid theorems of Euclidean geometry. We say that topological geometry is more abstract than projective geometry which is turn is more abstract than Euclidean geometry.

There had to be a route to follow that would lead one to think in such abstract spaces. Of course, one does not want to be divorced from reality. So one should not think that because the geometry of GR is understood, that you think nothing can come from the microseconds after the universe came into expression.

At this point in the development, although geometry provided a common framework for all the forces, there was still no way to complete the unification by combining quantum theory and general relativity. Since quantum theory deals with the very small and general relativity with the very large, many physicists feel that, for all practical purposes, there is no need to attempt such an ultimate unification. Others however disagree, arguing that physicists should never give up on this ultimate search, and for these the hunt for this final unification is the ‘holy grail’. Michael Atiyah

The Holy Grail sure comes up lots doesn't it:) Without invoking the pseudoscience that Peter Woit spoke of. I thought, if they could use Babar, and Alice then I could use the Holy Grail?

See more info on Coxeter here.

Like Peter I will have to address the "gut feelings" and the way Clifford expressed it. I do not want to practise pseudoscience as Peter is about the landscape.:)



When ones sees the constituent properties of that Gossett polytope 4₂₁ in all it's colours, the complexity of that situation is quite revealing. Might we not think in the time of supergravity, gravity will become weak, in the matter constitutions that form.

As in Neutrino mixing I am asking you to think of the particles as sound as well as think them in relation to the Colour of Gravity. If you were just to see grvaity in it's colourful design and what value that gravity in face of the photon moving within this gravitational field?

We detect the resulting "wah-wah-wah" in properties of the neutrino that appear and disappear. For example, when neutrinos interact with matter they produce specific kinds of other particles.

For example, when neutrinos interact with matter they produce specific kinds of other particles. Catch the neutrino at one moment, and it will interact to produce an electron. A moment later, it might interact to produce a different particle. "Neutrino mixing" describes the original mixture of waves that produces this oscillation effect.

The "geometry of curvature" had to be implied in the outcome, from that quantum world? Yet at it's centre, what is realized? You had to be lead there in terms of particle research to know that you are arriving at the "crossover point." The superfluid does this for examination.

5. Regular polytope: If you keep pulling the hypercube into higher and higher dimensions you get a polytope. Coxeter is famous for his work on regular polytopes. When they involve coordinates made of complex numbers they are called complex polytopes.

Pasquale Del Pezzo, Duke of Cajanello, (1859–1936), was "the most Neapolitan of Neapolitan Mathematicians".

He was born in Berlin (where his father was a representative of the Neapolitan king) on 2 May 1859. He died in Naples on 20 June 1936. His first wife was the Swedish writer Anne Charlotte Leffler, sister of the great mathematician Gösta Mittag-Leffler (1846-1927).

At the University of Naples, he received first a law degree in 1880 and then in 1882 a math degree. He became a pre-eminent professor at that university, teaching Projective Geometry, and remained at that University, as rector, faculty president, etc.

He was mayor of Naples starting in 1919, and he became a senator in the Kingdom of Naples.

His scientific achievements were few, but they reveal a keen ingenuity. He is remembered particularly for first describing what became known as a Del Pezzo surface. He might have become one of the strongest mathematicians of that time, but he was distracted by politics and other interests.

So what chance do we have, if we did not think this geometry was attached to processes that would unfold into the bucky ball or the fullerene of science. To say that the outcome had a point of view that is not popular. I do not count myself as attached to any intelligent design agenda, so I hope people will think I do not care about that.

NATHAN MYHRVOLD

I found the email debate between Smolin and Susskind to be quite interesting. Unfortunately, it mixes several issues. The Anthropic Principle (AP) gets mixed up with their other agendas. Smolin advocates his CNS, and less explicitly loop quantum gravity. Susskind is an advocate of eternal inflation and string theory. These biases are completely natural, but in the process the purported question of the value of the AP gets somewhat lost in the shuffle. I would have liked more discussion of the AP directly

See here for more information

So all the while you see the complexity of that circle and how long it took a computer to map it, it has gravity in it's design, whether we like to think about it or not?

But of course we are talking about the symmetry and any thing less then this would have been assign a matter state, as if symmetrical breaking would have said, this is the direction you are going is what we have of earth?

Isostatic Adjustment is Why Planets are Round?

While one thinks of "rotational values" then indeed one would have to say not any planets is formed in the way the sun does. Yet, in the "time variable understanding" of the earth, we understand why it's shape is not exactly round.



Do you think the earth and moon look round if your were considering Grace?

On the moon what gives us perspective when a crater is formed to see it's geological structure? It's just not a concern of the mining industry, as to what is mined on other orbs, but what the time variable reveals of the orbs structure as well.



Clementine color ratio composite image of Aristarchus Crater on the Moon. This 42 km diameter crater is located on the corner of the Aristarchus plateau, at 24 N, 47 W. Ejecta from the plateau is visible as the blue material at the upper left (northwest), while material excavated from the Oceanus Procellarum area is the reddish color to the lower right (southeast). The colors in this image can be used to ascertain compositional properties of the materials making up the deep strata of these two regions. (Clementine, USGS slide 11)

See more here

IN Search of Mandelstam's Holy Grail

There are two posts that reflect the purpose of this post today. One is Clifford's linked through Lee Smolin's comment and the other, at Backreaction. Good Physics is Conflict

A lot of you may never understand the significance of the mystery that follows the thinking of the Holy Grail. Yet is it more the knowledge that can be gained from all soul's day, that on this occasion we may have called it Halloween.

We celebrated the past, in the living of today? You philosophize, while you become the thoughts of models created by science leaders shared? I do not think any have a "personality disorder" like I do:)

Lee Smolin:

Here is an example of the kind of question I found I needed a book to explore: what to think of the problems that arise from the need for higher dimensions in string theory, such as the problem of moduli stabilization and the vast number of static solutions. To approach this I read books on the early history of GR and unified field theories and learned that higher dimensional compactifications were explored many times between 1914 and 1984 and that close to the beginning these problems were appreciated and discussed by Einstein and others. I weave this story into my book because I find it useful when trying to judge how serious the present issues in string theory are to know how Einstein and many others struggled with the same issues over decades.

So of course when we think of the persons of science who walked before us (shoulders of giants), what are their whole stories, but what is evidenced to us as we read those words? So you compile your data accordingly, and from it, we say at certain spots, how are we to react to the challenge now facing us?



Stanley Mandelstam, Professor Emeritus, Particle Theory

My present research concerns the problem of topology changing in string theory. It is currently believed that one has to sum over all string backgrounds and all topologies in doing the functional integral. I suspect that certain singular string backgrounds may be equivalent to topology changes, and that it is consequently only necessary to sum over string backgrounds. As a start I am investigating topology changes in two-dimensional target spaces. I am also interested in Seiberg-Witten invariants. Although much has been learned, some basic questions remain, and I hope to be able at least to understand the simpler of these questionsStanley Mandelstam-Professor Emeritus Particle Theory

As a lay person watching the debate it is difficult for me to discern the basis of these arguments. But I strive to go past what you think is surface in conduct in science's response, as some may show of themself in a reactionary pose. Should we all be so perfect, that the human condition is not also the example by which we shall progress in science?

Dealing in the Abstract



A sphere with three handles (and three holes), i.e., a genus-3 torus.

Of course the thinking may seem so detached from reality that one asks for some reason with which to believe anything. It required, that the history of this approached dust off models in glass cabinets, that were our early descendants of the museum today.

Sylvester's models lay hidden away for a long time, but recently the Mathematical Institute received a donation to rescue some of them. Four of these were carefully restored by Catherine Kimber of the Ashmolean Museum and now sit in an illuminated glass cabinet in the Institute Common Room.

How many of you know how to work in such abstract spaces, and know that what you are talking about has it's relationships in the physics of today? Or that, what satellites we use in measure of, have some correlation to how one may have seen "UV coordinates supplied by Gauss?"

Ways IN which To Percieve Landscape?

What a Cosmologist Wants from a String Theorist?




Emotion versus Reason?

3.1 As Cytowic notes, Plato and Socrates viewed emotion and reason as in a kind of struggle, one in which it was vitally important for reason to win out. Aristotle took a more moderate view, that both emotion and reason are integral parts of a complex human soul--a theory proposed by Aristotle in explicit opposition to Platonism (De Anima 414a 19ff). Cytowic appears to endorse the Platonic line, with the notable difference that he would apparently rather have emotion win out.

Emotion can be used as a catelysct into higher abstractual/dimensional thinking, if, it can be used to counter research into?:)

Figure 2. Clebsch's Diagonal Surface: Wonderful.

Mein Gott. :) If seeing on distance scales, had relevances in regards to "all the issues" of the standard model, would this not in effect change the way we see in those distances?

Peter Woit:I’ve looked very carefully in landscape papers and Susskind’s book for any sort of plausible idea about how this stuff will ever lead to a prediction of anything and I can’t find it.

Thanks Peter, that's it?


The Hills are Alive with the Sound of M theory?

With the discovery of sound waves in the CMB, we have entered a new era of precision cosmology in which we can begin to talk with certainty about the origin of structure and the content of matter and energy in the universeWayne Hu

By exercising the imagination I thought Wayne Hu did a fine job of relating these things on a "cosmological scale." Hills and Valleys. But in a more detailed quantum look, what value, conformal field theory of point particles?

In effect, the 5-D universe is recorded like a hologram on the 4-D surface at its periphery. Superstring theory rules in the 5-D spacetime, but a so-called conformal field theory of point particles operates on the 4-D hologram. A black hole in the 5-D spacetime is equivalent to hot radiation on the hologram--for example, the hole and the radiation have the same entropy even though the physical origin of the entropy is completely different for each case. Although these two descriptions of the universe seem utterly unalike, no experiment could distinguish between them, even in principle.

Les Houches




ROBBERT DIJKGRAAF:Map of the world, as used in my Les Houches lectures

I like this picture better Clifford. Is the landscape, as barren, or is it, the hope that we see such beautiful things of which the seed bed wil allow such things to arise from it?

For some, the "creative" outlet? Maybe, a Shangri-la high" in the mountains of abstractual thinking?

IN the Wunderkammern

James Joseph Sylvester (September 3, 1814 - March 15, 1897) was an English mathematician and lawyer.

We are told that "mathematics is that study which knows nothing of observation..." I think no statement could have been more opposite to the undoubted facts of the case; that mathematical analysis is constantly invoking the aid of new principles, new ideas and new methods, not capable of being defined by any form of words, but springing direct from the inherent powers and activity of the human mind, and from continually renewed introspection of that inner world of thought of which the phenomena are as varied and require as close attention to discern as those of the outer physical world, ...that it is unceasingly calling forth the faculties of observation and comparison, that one of its principal weapons is induction, that it has frequent recourse to experimental trial and verification, and that it affords a boundless scope for the exercise of the highest efforts of imagination and invention. ...Were it not unbecoming to dilate on one's personal experience, I could tell a story of almost romantic interest about my own latest researches in a field where Geometry, Algebra, and the Theory of Numbers melt in a surprising manner into one another.

While I always point upward in Rapheal's painting, I mention often, the "One thing."

Gold or wisdom, while leadng "the alchemist" in the search of that elucive material, mining, has to note the glimmer's as a sun shines on the landscape of ideas. So you work it, use a sluicebox, or a gold pan. Watch how river flow's and the bends in it. Where some deposits might have laid themself while others are carried off further down stream, left to some "eddie" or "pool of thinking." See flowers emerge in rocks crevices of all places.

However, don't be fooled! The charm of the golden number tends to attract kooks and the gullible - hence the term "fool's gold". You have to be careful about anything you read about this number. In particular, if you think ancient Greeks ran around in togas philosophizing about the "golden ratio" and calling it "Phi", you're wrong. This number was named Phi after Phidias only in 1914, in a book called _The Curves of Life_ by the artist Theodore Cook. And, it was Cook who first started calling 1.618...the golden ratio. Before him, 0.618... was called the golden ratio! Cook dubbed this number "phi", the lower-case baby brother of Phi.

See:

Fool's Gold

The Alchemist in You

String Theory Displays Golden Ratio Tendency

Special holonomy manifolds in string theory

So what instigated my topic today and Hypercharge make sits way for me to reconsider, so while doing this the idea of geoemtries and th eway in which we see this uiverse held to the nature of it's origination are moving me to consider how we see in ths geometrical sense.

The resurgence of ideas about the geometries taking place are intriguing models to me of those brought back for viewing in the Sylvester surfaces and B field relations held in context of the models found in the >Wunderkammern.

This paragraph above should orientate perception for us a bit around methods used to see in ways that we had not seen before. This is always very fascinating to me. What you see below for mind bending, helps one to orientate these same views on a surface.



Hw would you translate point on a two dimensional surface to such features on the items of interest on these models proposed?



Part of my efforts at comprehension require imaging that will help push perspective. In this way, better insight to such claims and model methods used, to create insight into how we might see those extra 10 dimensions, fold into the four we know and love.



G -> H -> ... -> SU(3) x SU(2) x U(1) -> SU(3) x U(1).

Here, each arrow represents a symmetry breaking phase transition where matter changes form and the groups - G, H, SU(3), etc. - represent the different types of matter, specifically the symmetries that the matter exhibits and they are associated with the different fundamental forces of nature

If one held such views from the expansitory revelation, that our universe implies at these subtle levels a quantum nature, then how well has our eyes focused not only on the larger issues cosmology plays, but also, on how little things become part and parcel of this wider view? That the quantum natures are very spread, out as ths expansion takes place, they collpase to comsic string models or a sinstantaneous lightning strikes across thei universe from bubbles states that arose from what?

So knowing that such features of "spherical relation" extended beyond the normal coordinates, and seeing this whole issue contained within a larger sphere of influence(our universe), gives meaning to the dynamical nature of what was once of value, as it arose from a supersymmetrical valuation from the origination of this universe? If Any symmetry breaking unfolds, how shall we see in context of spheres and rotations within this larger sphere, when we see how the dynamcial propertties of bubbles become one of the universes as it is today? Genus figures that arise in a geometrodynamcial sense? What are these dynacis within context of the sphere?



So as I demonstrate the ways in which our vision is being prep for thinking, in relation to the models held in contrast to the nature of our universe, how are we seeing, if we are moving them to compact states of existance, all the while we are speaking to the very valuation of the origination of this same universe?



Holonomy (30 Dec 2005 Wiki)

Riemannian manifolds with special holonomy play an important role in string theory compactifications. This is because special holonomy manifolds admit covariantly constant (parallel) spinors and thus preserve some fraction of the original supersymmetry. Most important are compactifications on Calabi-Yau manifolds with SU(2) or SU(3) holonomy. Also important are compactifications on G2 manifolds.

Foundational Mathematics and Physics?

I reproduce the post written below to Peter's Quantum Gravity Commentary because that basis of determinations supported by John Baez, introduces a new line of thinking, that as a layman, forces me to think about mathematics and physics in their context.

John Baez:

In short: it may be less important to work on physics when there’s a high chance one is barking up the wrong tree and ones work will wind up in the dustbin of history, than to do math that’s clearly good.

This issue, of course, is part of what Peter’s blog is all about
But, I understand the disappointed feelings you are expressing, because physics is a wonderful quest. It’s very hard to give it up, even in times like ours when it’s hard to tell if real progress is being made..

As the thinking of General Relativity unfolded I could not help to consider the developement of geometry through this process. Now, we have interesting physics experiments in relation cosmological questioons. Applicability of the enviroment to particle reductionism and collisions( see Steven Gidding here on blackhole production, or Pierre Auger experiments spoken to by John Ellis) in a modern world.

Corections made here in post after seeing no post their on Peter Woit's site>

Interesting ways in which to measure gravitational deviations?

So do we say, no gravitational differences exist? Two avenues to exploration make themself known and also the question of how we might see landscape abilities spread through interactive phases at levels of energy detrminations that warrant such views relative to physics developement and mathematical forays? I am getting confused.


John Baez said: The existence, number, and character of supergravity theories depends strongly on the dimension of spacetime!

http://www.lns.cornell.edu/spr/2001-07/msg0033897.html

John, you point out the basis of Peter's Blog and assert the basis of math as a lone venture outside of physics. Might it be concievable, that math should have the basis of physics at it's core, as it extends itself in those abtract realms?

Ex:

IN Sylvester surfaces, while it seems these shapes "beautiful", it would have not made more sense if the Dynkin diagrams, a introduction by Nigel Hitchens, would help us see B Field manifestation as interesting outside of the physics, yet related?

In a QG atmosphere, such landscape applicabiltiy would help extend concept developement to math relations you speak of in different weeks?

B Field Manifestations

Ah what the heck......I'll bite....let the skeptics converge in a harmonic convergence:)

Nigel Hitching

Sylvester Surfaces and the B field?

Are you a "gold fish" or a "Ant world person?" Are you a pigeon? Have you sent your vision into the things of nature, to explore it's potential in other ways?



Figure 2. Clebsch's Diagonal Surface: Wonderful

Rupert SheldarkeThe morphic fields of mental activity are not confined to the insides of our heads. They extend far beyond our brain though intention and attention. We are already familiar with the idea of fields extending beyond the material objects in which they are rooted: for example magnetic fields extend beyond the surfaces of magnets; the earth’s gravitational field extends far beyond the surface of the earth, keeping the moon in its orbit; and the fields of a cell phone stretch out far beyond the phone itself. Likewise the fields of our minds extend far beyond our brains.

The Faraday's, the Gauss's, the Reimanns learnt to see in other ways? Does this imply some spooky valuation beyond the confines of the brain's home?

"The gravitons behave like sound in a metal sheet," says Dvali. "Hitting the sheet with a hammer creates a sound wave that travels along its surface. But the sound propagation is not exactly two-dimensional as part of the energy is lost into the surrounding air. Near the hammer, the loss of energy is small, but further away, it's more significant."

So is it just a brain thingy, or is this "field real?" Some were not so unintelligent to "refute the aether" at one time. For we now understand what exists in the real spacetime valuations, beyond what is held to the brane, and see bulk manifestation, as real and populated. AS a extension, beyond those surfaces.

The Sound of Billiard Balls

Savas Dimopoulos:

Here’s an analogy to understand this: imagine that our universe is a two-dimensional pool table, which you look down on from the third spatial dimension. When the billiard balls collide on the table, they scatter into new trajectories across the surface. But we also hear the click of sound as they impact: that’s collision energy being radiated into a third dimension above and beyond the surface. In this picture, the billiard balls are like protons and neutrons, and the sound wave behaves like the graviton.

Are we execising the brains ability to get this toposense and geoemtrical revelation beyond straight lines and distances between points?

So what is a chaldni plate?:) helps you to see how sound is of value beyond the confines Faradays magnetic field lines, as real effects of that same magnet, and resonant coupling points. Exercising the potential of banging metal, helps the mind point to other places too. Playing pool, does too?:)

Special Lagrangian geometry

Dr. Mark Haskins

On a wider class of complex manifolds - the so-called Calabi-Yau manifolds - there is also a natural notion of special Lagrangian geometry. Since the late 1980s these Calabi-Yau manifolds have played a prominent role in developments in High Energy Physics and String Theory. In the late 1990s it was realized that calibrated geometries play a fundamental role in the physical theory, and calibrated geometries have become synonymous with "Branes" and "Supersymmetry".

Special Lagrangian geometry in particular was seen to be related to another String Theory inspired phemonenon, "Mirror Symmetry". Strominger, Yau and Zaslow conjectured that mirror symmetry could be explained by studying moduli spaces arising from special Lagrangian geometry.

This conjecture stimulated much work by mathematicians, but a lot still remains to be done. A central problem is to understand what kinds of singularities can form in families of smooth special Lagrangian submanifolds. A starting point for this is to study the simplest models for singular special Lagrangian varieties, namely cones with an isolated singularity. My research in this area ([2], [4], [6]) has focused on understanding such cones especially in dimension three, which also corresponds to the most physically relevant case.

I am execising the geometrical tendencies here in how Sylvester surfaces might have revealled the interior space of a Reimann sphere( Calabi Yau rotations exemplified and complete), while these points located on the sphere's surface, brane, reveal a deeper interactive force within this sphere. Again I am learning to see here, hopefully it's right. The bloggers out there who work in this direction are most helpful, P.P Cook, Lubos Motl and others, who help point the way.

Differences in the gravitational forces speak directly to dimensional relevances In Lagrangian, by association to the energy valuations? Euclids postulate from 1-4, had to be entertained in a new way, from a non-euclidean world of higher dimensions? It was well evident that supergravity, would find solace in the four dimensional relevances of spacetime? How did Kaluza and Klein get there? Cylinders?

Yet the dynamical world of the way in which the satelitte can move through space helps one to adjust to how these dynamcial avenues can propel this satelitte through that same space. Circular orits chaotically predictable, yet quite diverse shown in the poincare model representation, shows how bizzare the ability of the Lagrangian points become. Can one see well with this new abstractual quality?

Einstein's equations connect matter and energy (the right-hand side) with the geometry of spacetime (the left-hand side). Each superscript stands for one of the 4 coordinates of spacetime; so what looks like one equation is actually 4 x 4 = 16 equations. But since some are repeated there are really 10 equations. Contrast this with the single gravitational law of Newton! That alone gives a hint of the complexity of these equations. Indeed, they are amongst the most difficult equations in science. Happily, however, some exact solutions have been found. Below we discuss one such exact solution, the first, found in 1916 by Karl Schwarzchild.

So it was important to understand how this view was developed further. The semantics of mathematical expression was a well laid out path that worked to further our views of what could have been accompished in the world of spacetime, yet well knowing, that the dynamcial revealled a even greater potential?



So now you engaged the views inside and out, about bubble natures, and from this, a idea that is driven. That while Michio Kaku sees well from perspective, the bridge stood upon, is the same greater comprehension about abstract and dynamical processes in that same geometrical world. Beyond the sphere, within the sphere, and the relationship between both worlds, upon Lagrangian perspective not limited.

Placed within the sphere, and this view from a point is a amazing unfoldment process of views that topological inferences to torus derivtives from boson expressed gravitational idealizations removed themself from the lines of circles to greater KK tower representations?

The following is a description of some of the models for the hyperbolic plane. In order to understand the descriptions, refer to the figures. They may seem a bit strange. However, a result due to Hilbert says that it is impossible to smoothly embed the hyperbolic plane in Euclidean three-space using the usual Euclidean geometry. (Technical note: In fact it is possible to have a C^1 embedding into R^3, according to a 1955 construction of Nicolaas Kuiper, but according to William Thurston, the result would be "incredibly unwieldy, and pretty much useless in the study of the surface's intrinsic geometry."[William Thurston, "Three Dimensional Geometry and Topology," Geometry Center Preprint, 1991, p.43.]) Since there is no such smooth embedding, any model of the hyperbolic plane has to use a different geometry. In other words, we must redefine words like point, line, distance, and angle in order to have a surface in which the parallel postulate fails, but which still satisfies Euclid's postulates 1-4 (stated in the previous article). Here are brief descriptions of three models:

This process had to be thought of in another way? Point, line, plane, became something else, in terms of string world? M theory had to answer to the ideas of supergravity? How so? Great Circles and such? Topological torus forms defined, inside and out? Completed, when the circle become a boson expressed? A point on a brane now becomes something larger in perspectve? Thanks Ramond.

Wunderkammern

For me this is a wonderful view of abstraction, that had gone into model making, to help those less inclined to "the visonistic qualities of those same abstractions."

Shown here are the models in the mathematical wunderkammer located in the Department of Mathematics at the University of Arizona. Like those in most modern mathematics departments, the collection is a combination of locally-made student and faculty projects together with a variety of commercially produced models. Sadly, a century since their Golden Age, many of the models are in disrepair and much of their documentation has been lost. However, some recent detective work, with the help of the Smithsonian Institution in Washington, has helped the department identify models by the American educators W. W. Ross and R. P. Baker in the collection.

So having been allowed through internet developement to understand the work of fifth dimensional qualites could exist (why Thomas Banchoff must be added below), has far exceeded the understanding of those currently engaged in the mathematics? I do not mean to undermine or cast uncertainty in the direction of those who are helpijng us, but make for recognition of what technology has done for us, in the use of these internet capabilities.

Long before the advent of the World-Wide Web, Tom Banchoff was experimenting with ways of using electronic media to enhance mathematical research and aid in mathematical education. Banchoff helped install one of the first mathematics computer labs in the country, and continues to lead the development of innovative geometric software and curricula for undergraduate mathematics courses. He uses computer graphics as an integral part of his own research, and has used mathematical videos for the last 30 years as a means of disseminating his results.

I have been exploring these issues in regards to the Sylvester Surfaces, and the relationship seen in matrix development. It wasn't without some understanding that "isomorphic images" might have been revealled in orbital images categories, that dealing with this abstract world, didn't require some explanation?

The Magic Square



The picture below was arrived using the applet given from that site. What did you have do to change, in order to get the image I did? We are given possibilties?



But of course I am held by the physics of the world we see. As small as, might have exemplified itself in some larger cosmological imagery of a kind, can it be suited to topological features spoken too in string theory?

We know Max Tegmark has refuted the soccerball universe, and bazeian valuation of a quantum gravity model, that seem to good to be true? PLato, still felt that this soccer ball represented God? So maybe baezian, interpretaion, although derived from archimeadean, was more then the models through which they were precribed in Wunderkammen. Something ancient has been brought forward again for the mind bogglers that like to paly in these abstract spaces?

Mathematical Teaching Tools

Introduction: Lost Geometry

When I was small, growing up in Wisconsin, I loved to walk along the railroad tracks. As I walked, I would watch the steel rails grow from a point in the distance ahead of me, sweep around me, and then disappear again in the distance over my shoulder, converging slowly back to a point. The pure geometry of it was breathtaking. What impressed me the most, however, was the powerful metaphor that it suggested: How wide the present seemed, simply because of my presence there; how small the future and the past. And yet, I could move along the tracks, imagining myself expanding and contracting the infinite timeline of history. I could move ahead until any previous place along that continuum had shrunk to insignificance, and I could, despite the relentless directionality that I imagined moving along the tracks like so many schedule-bound trains, drift backwards as easily as I could let myself be carried forward.

The wonderful stories exemplifed by human experience, places me in states of wonder. About how processes in geometry could have engaged us in a real dialogue with nature's way around us. To see these stories exemplified above. One more that quickly came to mind, was Michio Kaku's view from the bridge, to the fish in the pond. Looking at the surface from two perspective sseem really quite amazing to me.

Such exchanges as these are wonderful exercises in the creation of the historical abstract. A Lewis Carroll in the making? An Abbotsolutely certainty of math structures, that we would like to pass on to our children and extend the nature to matter of the brain's mass?

Albrecht Durer and His Magic Square

Albrecht Dürer(self portrait at 28)

It was important to me that I post the correct painting and one that had undergone revision to exemplify the greater context of geometrical forms. In the Topo-sense? Artistic renditions help and adjust views, where information in mathematical minds, now explains something greater. Melencolia II
[frontispiece of thesis, after Dürer 1514]by Prof.dr R.H. Dijkgraaf

"Two images when one clicked on," shows what I mean.

Melancholia in 1514(the original)

The Magic Square

Like Pascal, one finds Albrecht has a unique trick, used by mathematicians to hide information and help, to exemplify greater contextual meaning. Now you have to remember I am a junior here in pre-established halls of learning, so later life does not allow me to venture into, and only allows intuitive trials poining to this solid understanding. I hope I am doing justice to learning.

A new perspective hidden in the Prof.dr R.H. Dijkgraaf
second rendition, and thesis image, reveals a question mark of some significance?:) So how would we see the standard model in some "new context" once gravity is joined with some fifth dimensional view?

Matrix developement?

Like "matrix developement," we see where historical significance leads into the present day solutions? How did such ideas manifest, and we look for this in avenues of today's science.

In 1931 Dirac gave a solution of this problem in an application of quantum mechanics so original that it still astounds us to read it today. He combined electricity with magnetism, in a return to the 18th-century notion of a magnet being a combination of north and south magnetic poles (magnetic charges), in the same way that a charged body contains positive and negative electric charges.

How relevant is this? How important this history? How relevant is it, that we see how vision has been extended from plates(flat surfaces to drawings) to have been exemplified in sylvester surfaces and object understanding. This goes much further, and is only limited by the views of those who do not wish to deal with higher dimensional ventures?



See:

Topo-sense

The Abstract World

Sylvester's Surfaces

Figure 2. Clebsch's Diagonal Surface: Wonderful.

We are told that "mathematics is that study which knows nothing of observation..." I think no statement could have been more opposite to the undoubted facts of the case; that mathematical analysis is constantly invoking the aid of new principles, new ideas and new methods, not capable of being defined by any form of words, but springing direct from the inherent powers and activity of the human mind, and from continually renewed introspection of that inner world of thought of which the phenomena are as varied and require as close attention to discern as those of the outer physical world, ...that it is unceasingly calling forth the faculties of observation and comparison, that one of its principal weapons is induction, that it has frequent recourse to experimental trial and verification, and that it affords a boundless scope for the exercise of the highest efforts of imagination and invention. ...Were it not unbecoming to dilate on one's personal experience, I could tell a story of almost romantic interest about my own latest researches in a field where Geometry, Algebra, and the Theory of Numbers melt in a surprising manner into one another.

I had been looking for the link written by Nigel Hitchin, as this work was important to me, in how Dynkin drawings were demonstrated. Although I have yet to study these, I wanted to find this link and infomration about James Sylvester, because of the way we might see in higher dimensional worlds.His model seem important to me from this perspective.

Sylvester's models lay hidden away for a long time, but recently the Mathematical Institute received a donation to rescue some of them. Four of these were carefully restored by Catherine Kimber of the Ashmolean Museum and now sit in an illuminated glass cabinet in the Institute Common Room.

The reason for this post is th ework dfirst demonstrated by Lubos Motl and th etalk he linked by Nigel Hitchin. The B-field, which seems to no longer exist, or maybe I am not seeing it in his posts archived?

In 1849 already, the British mathematicians Salmon ([Sal49]) and Cayley ([Cay49]) published the results of their correspondence on the number of straight lines on a smooth cubic surface. In a letter, Cayley had told Salmon, that their could only exist a finite number - and Salmon answered, that the number should be exactly 27

.

There had to be a simplification of this process, so in gathering information I hope to complete this, and gain in understanding.

James Joseph Sylvester (September 3, 1814 - March 15, 1897) was an English mathematician and lawyer.

Now as to the reason why this is important comes from the context of geometrical forms, that has intrigued me and held mathematicians minds. Sometimes it is not just the model that is being spoken too, but something about the natural world that needs some way in which to be explained. Again, I have no teachers, so I hope to lead into this in a most appropriate way, and hopefully the likes of those involved, in matrix beginnings, have followed the same process?

The 'Cubics With Double Points' Gallery




f(x,y,z) = x2+y2+z2-42 = 0,

i.e. the set of all complex x,y,z satisfying the equation. What happends at the complex point (x,i*y,i*z) for some real (x,y,z)?

f(i*x,y,z) = x2+(i*y)2+(i*z)2-42
= x2+i2*y2+i2*z2-42
= x2-y2-z2-42.

Has it become possible that you have become lost in this complex scenario? Well what keeps me sane is the fact that this issue(complex surfaces) needs to be sought after in terms of real images in the natural world. Now, I had said, the B-field, and what this is, is the reference to the magnetic field. How we would look at it in it's diverse lines? Since on the surface, in a flat world, this would be very hard to make sense of, when moved to the three coordinates, these have now become six?

fancier way of saying that is that in general, it's okay to model the space around us using the Euclidean metric. But the Euclidean model stops working when gravity becomes strong, as we'll see later.

Now what has happened below, is that what happens in quark to quark distances, somehow in my mind is translated to the values I see, as if in the metric world and moved to recognition of Gaussian curves and such, to decribe this unique perspective of the dynamics of Riemann, lead through geometrical comprehension ad expression. No less then the joining of gravity to Maxwells world.

Like the magnetic field we know, the lines of force represent a dynamcial image, and so too, how we might see this higher dimensional world. Again I don't remember how I got here, so I am trying hard to pave this road to comprehension.



"Of course, if this third dimension were infinite in size, as it is in our world, then the flatlanders would see a 1/r2 force law between the charges rather than the 1/r law that they would predict for electromagnetism confined to a plane. If, on the other hand, the extra third spatial dimension is of finite size, say a circle of radius R, then for distances greater than R the flux lines are unable to spread out any more in the third dimension and the force law tends asymptotically to what a flatlander physicist would expect: 1/r.

However, the initial spreading of the flux lines into the third dimension does have a significant effect: the force appears weaker to a flatlander than is fundamentally the case, just as gravity appears weak to us.

Turning back to gravity, the extra-dimensions model stems from theoretical research into (mem)brane theories, the multidimensional successors to string theories (April 1999 p13). One remarkable property of these models is that they show that it is quite natural and consistent for electromagnetism, the weak force and the inter-quark force to be confined to a brane while gravity acts in a larger number of spatial dimensions."

Now here to again, we are exercising our brane function(I mean brain)in order to move analogies to instill views of the higher dimensional world. The missing energy had to go somewhere and I am looking for it?:) So ideas like "hitting metal sheets with a hammer", or "billiards balls colliding", and more appropriately so, reveal sound as a manifestation of better things to come in our visions?

See:

Unity of Mathematics