Sound of two Black Holes Colliding

The New York Times · The Sound of Two Black Holes Colliding

The Sound of the Perfect Fluid

 

 The sound of the perfect fluid

 

Perfect fluid

From Wikipedia, the free encyclopedia

Jump to navigation Jump to search

The stress–energy tensor of a perfect fluid contains only the diagonal components.

In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame mass density ${\displaystyle \rho _{m}}$ and isotropic pressure p.

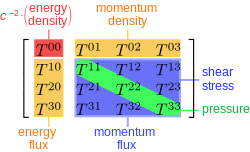
Real fluids are "sticky" and contain (and conduct) heat. Perfect fluids are idealized models in which these possibilities are neglected. Specifically, perfect fluids have no shear stresses, viscosity, or heat conduction.

In space-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form

${\displaystyle T^{\mu \nu }=\left(\rho _{m}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }+p\,\eta ^{\mu \nu }\,}$

where U is the 4-velocity vector field of the fluid and where ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (-1,1,1,1)}$ is the metric tensor of Minkowski spacetime.

In time-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form

${\displaystyle T^{\mu \nu }=\left(\rho _{\text{m}}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }-p\,\eta ^{\mu \nu }\,}$

where U is the 4-velocity of the fluid and where ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (1,-1,-1,-1)}$ is the metric tensor of Minkowski spacetime.

This takes on a particularly simple form in the rest frame

${\displaystyle \left[{\begin{matrix}\rho _{e}&0&0&0\\0&p&0&0\\0&0&p&0\\0&0&0&p\end{matrix}}\right]}$

where ${\displaystyle \rho _{\text{e}}=\rho _{\text{m}}c^{2}}$ is the energy density and ${\displaystyle p}$ is the pressure of the fluid.

Perfect fluids admit a Lagrangian formulation, which allows the techniques used in field theory, in particular, quantization, to be applied to fluids. This formulation can be generalized, but unfortunately, heat conduction and anisotropic stresses cannot be treated in these generalized formulations.^[why?]

Perfect fluids are used in general relativity to model idealized distributions of matter, such as the interior of a star or an isotropic universe. In the latter case, the equation of state of the perfect fluid may be used in Friedmann–Lemaître–Robertson–Walker equations to describe the evolution of the universe.

In general relativity, the expression for the stress–energy tensor of a perfect fluid is written as

${\displaystyle T^{\mu \nu }=\left(\rho _{m}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }+p\,g^{\mu \nu }\,}$

where U is the 4-velocity vector field of the fluid and where ${\displaystyle g_{\mu \nu }}$ is the metric, written with a space-positive signature.

See also

• Equation of state
• Ideal gas
• Fluid solutions in general relativity
• Potential flow

References

• The Large Scale Structure of Space-Time, by S.W.Hawking and G.F.R.Ellis, Cambridge University Press, 1973. ISBN 0-521-20016-4, ISBN 0-521-09906-4 (pbk.)

External links

• Mark D. Roberts, [A Fluid Generalization of Membranes http://www.arXiv.org/abs/hep-th/0406164 hep-th/0406164].

Past String Conferences

 

 

Strings 2019, Brussels, Belgium
Strings 2018, Okinawa, Japan
Strings 2017, Israel
Strings 2016, Beijing, China
Strings 2015, Bengaluru, India
Strings 2014, Princeton, USA
Strings 2013, Seoul, Korea
Strings 2012, Munich, Germany
Strings 2011 Uppsala, Sweden
Strings 2010 Texas, USA
Strings 2009, Rome, Italy
Strings 2008, CERN, Switzerland
Strings 2007, Madrid, Spain
Strings 2006, Beijing, China
Strings 2005, Toronto, Canada
Strings 2004, Paris, France
Strings 2003, Kyoto, Japan
Strings 2002, Cambridge, United Kingdom
Strings 2001, Mumbai, India
Strings 2000, Ann Arbor, USA
Strings 1999, Potsdam, Germany
Strings 1998, Santa Barbara, USA
Strings 1997, Amsterdam, The Netherlands
Strings 1996, Santa Barbara, USA
Strings 1995, Los Angeles, USA